2022年05月24日 力扣每日一题

675. 为高尔夫比赛砍树

题目

你被请来给一个要举办高尔夫比赛的树林砍树。树林由一个 m x n 的矩阵表示， 在这个矩阵中：

• 0 表示障碍，无法触碰
• 1 表示地面，可以行走
• 比 1 大的数 表示有树的单元格，可以行走，数值表示树的高度

每一步，你都可以向上、下、左、右四个方向之一移动一个单位，如果你站的地方有一棵树，那么你可以决定是否要砍倒它。

你需要按照树的高度从低向高砍掉所有的树，每砍过一颗树，该单元格的值变为 1（即变为地面）。

你将从 (0, 0) 点开始工作，返回你砍完所有树需要走的最小步数。 如果你无法砍完所有的树，返回 -1 。

可以保证的是，没有两棵树的高度是相同的，并且你至少需要砍倒一棵树。

示例 1：

  
输入：forest = [[1,2,3],[0,0,4],[7,6,5]]  
输出：6  
解释：沿着上面的路径，你可以用 6 步，按从最矮到最高的顺序砍掉这些树。

示例 2：

  
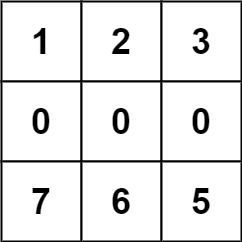
输入：forest = [[1,2,3],[0,0,0],[7,6,5]]  
输出：-1  
解释：由于中间一行被障碍阻塞，无法访问最下面一行中的树。  

示例 3：

  
输入：forest = [[2,3,4],[0,0,5],[8,7,6]]  
输出：6  
解释：可以按与示例 1 相同的路径来砍掉所有的树。  
(0,0) 位置的树，可以直接砍去，不用算步数。  

提示：

• m == forest.length
• n == forest[i].length
• 1 <= m, n <= 50
• 0 <= forest[i][j] <= 109

思路

1. 记录每颗需要砍树的位置，并排好序

   注意：这个需要砍的树是从2开始算的，不是1

2. 循环计算到达下一棵被砍树的步数

   可使用广度优先搜索，从出发的树开始，依次取出并将下一步能够到达的树加入到队列，直到目标树为止

代码

java：

class Solution {
    public int cutOffTree(List<List<Integer>> forest) {
        /*
        起始位置不可到达的情况，即坐标（0,0）位置为0
         */
        if (forest.get(0).get(0) == 0) {
            return -1;
        }
        int xL = forest.size();
        int yL = forest.get(0).size();
        /*
        按照顺序排列需要砍的树，记录每棵树的位置
         */
        TreeMap<Integer, Pair<Integer, Integer>> map = new TreeMap<>();
        for (int i = 0; i < xL; i++) {
            List<Integer> list = forest.get(i);
            for (int j = 0; j < yL; j++) {
                if (list.get(j) > 1) {
                    map.put(list.get(j), new Pair<>(i, j));
                }
            }
        }
        int step = 0;
        Pair<Integer, Integer> pair = null;
        Queue<Pair<Integer, Integer>> queue = new LinkedList<>();
        queue.add(new Pair<>(0, 0));
        boolean[][] uses = new boolean[xL][yL];
        uses[0][0] = true;
        int[] xs = new int[]{1, -1, 0, 0};
        int[] ys = new int[]{0, 0, 1, -1};
        for (int key : map.keySet()) {
            Pair<Integer, Integer> cur = map.get(key);
            if (queue.peek().equals(cur)) {
                continue;
            }
            boolean bl = false;
            /*
            计算到达下一棵需要砍树的步数
             */
            while (!queue.isEmpty() && !bl) {
                int nums = queue.size();
                step++;
                for (int i = 0; i < nums && !bl; i++) {
                    Pair<Integer, Integer> tmp = queue.poll();
                    for (int j = 0; j < 4; j++) {
                        int x = tmp.getKey() + xs[j];
                        int y = tmp.getValue() + ys[j];
                        if (x == cur.getKey() && y == cur.getValue()) {
                            bl = true;
                            break;
                        }
                        if (x < 0 || x >= xL || y < 0 || y
                                >= yL || uses[x][y] || forest.get(x).get(y
                            continue;
                        }
                        queue.add(new Pair<>(x, y));
                        uses[x][y] = true;
                    }
                }
            }
            if (!bl) {
                return -1;
            }
            queue = new LinkedList<>();
            queue.add(cur);
            uses = new boolean[xL][yL];
            uses[cur.getKey()][cur.getValue()] = true;
        }
        return step;
    }
}